4. Medidas de Tendencia Central

 

Indicador de Calidad

• Reconoce la media, mediana y moda, en la representación de un conjunto de datos.

• Compara, usa e interpreta datos que provienen de situaciones reales, y traduce entre diferentes representaciones de un conjunto de datos.

Metodología de Clase

• Ambientación - Motivación inicial

¿Por qué es importante establecer la media dentro de un conjunto de datos?

Den ejemplos en donde se utilice la media.

• Retroalimentación del tema

Definición

Las medidas de tendencia central son valores que se ubican al centro de un conjunto de datos ordenados según su magnitud.

Las medidas de tendencia central, son empleadas, para resumir a los conjuntos de datos, que serán sometidos a un estudio estadístico.

MEDIA (promedio) X

La media estadística, es una medida de tendencia central, que obtiene el promedio de los datos tabulados; también es conocida como media aritmética, y se obtiene:

1. Sumando todos los números juntos
2. Divide por la cantidad de números que fueron sumados.

Ejemplo

¿Cuál es la media de las edades de Andrea y sus primos?

Imagen tomada de Portaleducativo

MEDIANA (mediana) Me

Imagen tomada de Universoformulas

La mediana estadística, representa el número central de un grupo de números ordenados por tamaño. 

Imagen tomada de Josemanuelcremades

Si la cantidad de datos es par, la mediana es el promedio de los dos números centrales. Si es impar, la mediana es el valor central.

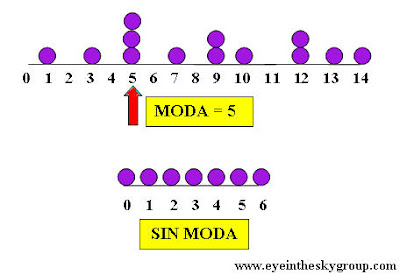
MODA (Moda) Mo

La moda estadística, es el valor que más se repite en un grupo de valores. 

Se obtiene:

1. Ordena los números según su tamaño
2. Determina la cantidad de veces de cada valor numérico
3. El valor numérico que más se repite es la moda

Puede haber más de una moda cuando dos o más números se repiten la misma cantidad de veces y además éste es el máximo número de veces del conjunto.

No hay moda si ningún número se repite más de una vez.

Actividad de clase No. 1  - Práctica individual en cuaderno

Desarrollar la siguiente actividad en el cuaderno:

Actividad de clase No. 2  - Pruebas saber

Ingrese al siguiente formulario

Actividad de clase No. 3  - Ejercicios en Excel

• El número de diás necesarios por 10 equipos de trabajadores para terminar 10 instalaciones de iguales características han sido: 21, 32, 15, 59, 60, 61, 64, 60, 71, y 80 días. Calcular la media, mediana, moda.

• Se lanza un dado 19 veces con las siguientes lecturas: 5, 1, 3, 3, 6, 2, 6, 4, 5, 2, 1, 2, 5, 3, 2, 6, 1, 4, 4

a) ¿Cuál es el promedio de las lecturas obtenidas?

b) ¿Cuál es la tirada que más se repite?

c) ¿Cuál es el mayor valor intermedio de todas las lecturas,             ordenadas estas de menor a mayor?

• En clase de inglés 10 alumnos han sacado la siguientes notas: 7, 6.5, 4, 1, 9, 5, 8, 8.5, 2, 5.5.  Calcular la moda, mediana y media aritmética.

• Calcular la media, la mediana y la moda de la siguiente serie de números: 5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.

• En un examen calificado del 0 al 10, 3 personas obtuvieron 5 de nota, 5 personas obtuvieron 4 de nota, y 2 personas obtuvieron 3 de nota. Calcular la nota media, la mediana y la moda.

MARIA LUCIA CESPEDES

Docente Informática

Grado Décimo